Joel's dev blog

Memoization in python using a decorator: getting a prime number

May 05, 2019

⏳ 4 min read

Rationale

I was creating an isPrime function:

def isPrime(n):
    prime = [True for i in range(n + 1)]
    fac = 2
    while fac * fac <= n + 1:
        if prime[fac]:
            for i in range(fac*fac, n + 1, fac):
                prime[i] = False
        fac += 1
    return prime[n]

Time complexity

For now, forget about the condition in the while loop: fac * fac <= n + 1. You know that you are going to fill out the array of size n anyways. This is going to take O(n) time (prime[i] = False run at least n times overall).

And the tricky part is for i in range(fac*fac, n + 1, fac):. It is going to take less than O(nlogn) time. This is because if you compare this series with a harmonic series:

  • Harmonic: 1 + 1/2 + 1/3 + 1/4 + 1/5 + … + 1/n
  • for i in range(fac*fac, n + 1, fac): you have to run at least about n + 1 / fac ~= n / fac times. So each time you are going to get 1/2 + 1/3 + 1/5 + 1/7 … + n/n.

Now, obviously, the number of calculation of harmonic series of a given n is greater than that of a series of reciprocals of prime numbers up to n.

Harmonic series has a time complexity of nlogn.

or, better, a series of reciprocals of prime numbers has a time complexity of nloglogn.. I will cut the explanation off here for now because it is going to be too complex.

Anyways, so if you add up: O(n) + O(nloglogn) = O(nloglogn) as you can discard the same term with a smaller multiple.

So the time complexity of this algorithm, called Sieve of Eratosthenes, has a time complexity of O(nloglogn) (this many arithmetic operations will happen).

Graph

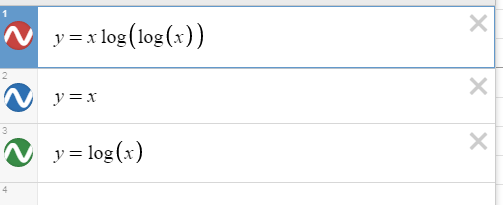
Legend

See that xlog(log(x)) is O(x), but xlog(log(x)) grows much faster than log(x).

So you may.. think of caching.

Ok. So that was the main rationale for memoization. Sorry for the rationale being too long.

So let’s see how we can memoize.

Memoization

A decorator is just a higher-order function. Takes in a function as a parameter and outputs a function with some additional functionalities.

A normal decorator may look like this:

def memoize(func):
    cache = {}

    def memoizer(*args, **kwargs):
        key = str(args) + str(kwargs)
        if key not in cache:
            cache[key] = func(*args, **kwargs)
        return cache[key]

    return memoizer

Note that cache won’t be permitted to be accessed inside memoizer if it is not a mutable object: for example, int. If you want to enable it, you should go for nonlocal.

So this is the memoized version of getting prime numbers. I fixed the previous code to enable memoization of a list.

from typing import List, Callable

intToList = Callable[[int], List[int]]

def memoize(func : intToList) -> intToList:
    cache = []
    def memoizer(n):
        nonlocal cache
        if n > len(cache): # haven't met this n before
            cache = func(n) # if new, calculate from scratch again
        return cache 
    return memoizer

@memoize
def getPrime(n : int) -> List[int]:
    prime = [True for i in range(n + 1)]
    fac = 2
    while fac * fac <= n + 1:
        if prime[fac]:
            for i in range(fac*fac, n + 1, fac):
                prime[i] = False
        fac += 1
    return prime

Fair enough. A true memoization would detect that n is bigger than len(cache), so that calculation runs only from len(cache) to n. But that requires more adjustments to the code. For now, I decided to be complacent with this: if you enter n that is less than any previous inputs, getPrime is just going to return cache.

So this is an actual usage with isPrime:

from typing import List, Callable

intToList = Callable[[int], List[int]]

def memoize(func : intToList) -> intToList:
    print('with memoize')
    cache = []
    def memoizer(n):
        nonlocal cache
        if n > len(cache): # haven't met this n before
            cache = func(n) # if new, calculate from scratch again
        return cache 
    return memoizer

@memoize
def getPrime(n : int) -> List[int]:
    prime = [True for i in range(n + 1)]
    fac = 2
    while fac * fac <= n + 1:
        if prime[fac]:
            for i in range(fac*fac, n + 1, fac):
                prime[i] = False
        fac += 1
    return prime

def isPrime(n : int) -> bool:
    return getPrime(n)[n]

if __name__ == '__main__':
    import timeit
    script = "isPrime(20)\nisPrime(17)\nisPrime(10)"             
    print(timeit.timeit(script, setup="from __main__ import isPrime"))

Remember, timeit by default runs 1000000 times of execution.

timeit gave this result:

With @memoize Without @memoize
Result (1000000 executions) 1.5277864220000001 14.473305422

Wow. It’s gotta be a must. It’s really much faster… It should be.

Timeit Result

Sources

Written by Joel Mun. Joel likes Typescript, React, Node.js, GoLang, Python, Wasm and more. He also loves to enlarge the boundaries of his knowledge, mainly by reading books and watching lectures on Youtube. Guitar and piano are necessities at his home.

© Joel Mun 2023